Belli zaman dilimleri içinde belirli bir hareketin tekrarlanması
olayına salınım adı verilir.hepimizin bildiği salıncak bunun en çok
rastlanan örneğidir. Masanın kenarına sıkıştırdığımız jiletin titreşmesi veya
bir keman telinin titreşimi benzer salınım örnekleridir.

Daha bilimsel bir örnek bir basit sarkacın salınımıdır. Sarkacın salınımları,
denge konumundan sağa ve sola doğru belli uzaklıktadır. Eğer sürtünme kuvvetleri
olmasaydı bu şekilde salınan sarkaç genliğini hiç bozmadan aynı hareketi devamlı
olarak sürdürürdü.Sarkacın denge konumundan sağa veya sola sapması yani yön
değiştirmesi,salınım hareketinin en önemli  özelliğidir, buna genlik denir.
Sarkacın denge konumundan ayrılıp tekrar denge konumuna gelmesi hareketin
yarısını oluşturur. Tam bir salınım hareketi, sarkacın denge konumundan ayrılıp
bir yöne gittikten sonra, diğer yönde maksimum noktaya ulaşıp tekrar denge
konumuna gelmesidir, buna hareketin  'Peryot'u adı verilir. Saniyedeki peryot
sayısı ise 'Frekans'

olarak adlandırılır.

Sarkacın bu hareketini dairesel bir hareket kabul edersek,bir peryotluk bir
hareket sırasında bir çember etrafı dönülmüş olur ve bu  '2pr'
kadar bir yol demektir. Bu şekilde ki salınım hareketleri kartezyen koordinat
sisteminde  'x = a sin q' fonksiyonu şeklinde gösterililr.

Bir çember etrafında hareket eden bir noktanın bir turda aldığı yol 2pr
ve gördüğü açı 2p radyan olur.Birim zamanda görülen
açıya açısal hız  ( w )adı verilir.t saniyede taranan
açıdır.     w =  2 p /
t       olur.                    

T yani peryot ‘ un   1/f  olduğunu biliyoruz; çünkü peryot bir
hareketin süresi, frekans ise bir saniyedeki hareket sayısıdır.

f x T  =  1       dir. 

bir no'lu formülde ki   't' zamanı içinde bir hareket olduğu için,bir
hareketin zamanı olan peryot T yi bu eşitliğe koyabiliriz veya T yerine 1/f 'i
koyabiliriz . O halde;

w = 2 p f         olur.

X = a sin q da  q 
açısının yerine  wt yazabiliriz.

X = a sin w t 

X =  a sin 2 p f t        
dir.                      

Elektriğin bu şekilde salınan şekline Alternatif akım adı verilir.

Alternatif akım alternatör denilen cihazlarla elde edilir.

Alternatif akımın ve gerilimin formülü

U = Umax. Sin w. t

U = Umax. Sin 2p f t

 I =  I max .Sin w.t

 I =  I max .Sin 2p f t

Şeklinde yazılır.Akım ve gerilim aynı fazdadır. Bir bobin den geçerken akım
90 derece yani p/2 kadar geri kalır.

Bir kondansatör de ise bu sefer gerilim 90 derece yani  p
/ 2 kadar geridedir.

Alternatörler de manyetik alanda indüklenen bir bobin mevcuttur. Farklı
kutuplarda bobinin üzerinde oluşan akım yön değiştirir ve değişken bir elektrik
akımı ortaya çıkar. Bu şekilde ortaya çıkan elektrik A.C. olarak yazılan 
'Alternatif  Current'dır.

 

Bu çeşit elektrik, yön değiştirme özelliği nedeni ile
voltajı transformatörlerde yükseltilip  düşürülebilir. Bu sayede
yüksek voltajların daha az kayıpla nakledilmeleri sebebi ile A.C. uzak 

mesafelere daha az kayıpla nakledilebilir. Bugün evlerde ve sanayide
kullandığımız hep bu çeşit  elektriktir.

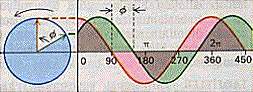Faz ve faz farkı

 

Evlerde 220 volt olarak kullandığımız A.C. etkin değer veya RMS değer
dediğimiz değerde bir alternatif akımdır.RMS (root-mean-square) değer A.C. nin,
bir resistor üzerinde tükettiği  enerjiye eşit enerji tüketen  D.C.
karşılığıdır.

Teorik olarak etkin değer'e eşit olan RMS değeri, Alternatif akım maximum
değer veya tepe değerinin karekökü alınarak bulunur.

Genelde bir A.C. den bahsedilirken hep etkin değerden bahsedilir. Ölçü
aletleri de bu değeri ölçerler.

A.C.  ın bir de ortalama değeri vardır. Ortalama değer pozitif veya negatif
saykıldaki ani değerlerinin toplamının ortalamasıdır.

Maximum değer 1 ise RMS 0.707  Ortalama değer ise 0.636'dır

FAZ : Bir Alternatif akımı veya gerilimi, koordinat
sisteminde gösterebileceğimizi ve bir hareketin yani peryodun 2p
olduğunu söylemiştik. Buradaki 2p bir haraket
süresince taranan açıdır.İkinci bir peryotta bir 2p
kadar daha açı taranır.Şimdi bir başka alternatif gerilim veya akımın bu
koordinat sisteminde 0 noktasından değil de p/2 
kadar ileriden harekete başladığını varsayalım işte iki hareket arasında mevcut
mesafe olan p/2 kadar farka faz farkı adı verilir.

Direnç, Kondansatör ve Bobin karşısında Alternatif akımın 

davranışı nasıldır ?

Resistansın ( direncin ) Alternatif akıma karşı davranışı D.C.
gibidir.Uçlarına A.C. uygulanmış Bir Resistor'ün gösterdiği direnç aynıdır.Ohm
yasası kullanılır.

Uçlarına A.C. uygulanmış bir bobinde “Endüktif devre “ durum değişiktir. Bu
bobin  uclarında bir zıt E.M.K oluşur. Bobinin indüktansı yanında bir de
resistansı söz konusudur eğer bu 

resistans sıfır değerde ise bu bobin devresi saf indüktif devre olarak
adlandırılır. Bobinin gösterdiği dirence ise "İndüktif Reaktans" adı verilir.

{Endüktif Reaktans  } X L = wL = 2
p f L      dir.                            

Seri ve paralel bağlamalarda  dirençler gibi aynı formüller kullanılır.

Bir bobine tatbik edilen A.C. da akım engelle karşılaşır ve geri kalır. Bu
nedenle bobinde akımla gerilim arasında 90 derece faz farkı vardır.

Uclarına bir A.C. tatbik edilmiş kondansatörde, yani kapasitif bir devrede ki
dirence "Kapasitif Reaktans" adı verilir.

{ Kapasitif Reaktans } Xc  = 1/ w. C         dir.

Xc  =  1/ 2p f C     dir.                                 

Burada değerler Ohm, Farad, Henry'dir. Bir kapasitif devrede gerilime zorluk
vardır ve gerilim 90 derece geri kalır.

Paralel kondansatörler de toplam kapasitif reaktans;

 

1/Xc= 1/ Xc1 +1/Xc2+1/Xc3 +..1/Xcn dir.

Seri bağlı kondansatörlerde ise toplam kapasitif reaktans  her kondansatörün
kapasitif reaktansları toplamıdır.

Xc = Xc1+Xc2+Xc3+….Xcn      dir.

Buraya kadar yalnız başına olan bobin, kondansatör ve direncin alternatif
akıma karşı olan davranışını ve gösterdiği direnci gördük, ama elektronik
devrelerde çoğu zaman bobin, kondansatör ve dirençler birlikte
kullanılırlar.İşte böyle hallerde yani; bobin, kondansatör, direnç gibi
elemanların, çeşitli şekilde bağlantılarında A.C. ye karşı gösterilen eşdeğer
dirence

'EMPEDANS'’ adı verilir. Z ile gösterilir.Klasik Ohm kanununda ki R direnci
yerine Z empedans değeri konarak, Alternatif akım devrelerinde Ohm kanunu
kullanılabilir.

V = I . Z       dir.

Seri devrelerde,devreden geçen akım sabittir. Gerilim ise her devre elemanı
uçlarında farklıdır. Bu nedenle seri devrelere 'Akım devresi' adı verilir ve
referans olarak akım alınır. Akım Koordinat sistemi üzerinde X ekseninde
gösterilir.

 

 

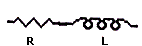Direnç Bobin seri devresi

 

 

Burada direnç uçlarındaki gerilim VR  = İ.R'dir

Bobin ucundaki gerilim;

VL  =  İ .XL'dir

Burada XL kullanılması nın nedeni, alternatif akım da bobinin direncinin
indüktans olarak karşımıza çıkmasıdır ve indüktans formülü kullanılır. Devrenin
uçlarındaki gerilim ise,

bunların vektörel toplamıdır.

          _____________

V =  V  VR² + VL²        olur.

Devrenin uçlarındaki gerilim

V = İ . Z  dir. O halde tüm V lerin yerine karşılıklarını yazarsak

            _______________

İ.Z = V(İ.R)² +(İ.XL)²     olur.

           _______________

Z =  V  R² + XL²        olur.               

Yukarıda seri bir direnç, bobin devresinde empedansı gördük,

burada bobinin gerilimi  90 derece ileri fazdadır. Direncin 

akımı ve gerilimi arasında bir faz farkı yoktur. Her iki gerilimin 

vektörel toplamları bu devrede gerilimin akıma göre j 
açısı 

kadar ileride olduğunu gösterir. Bu açı:

Cos j  =  R / Z dir. 

Bir direnç ve bir kondansatörden oluşan seri bir devrede durum nasıldır ?

Bu devrede kondansatör gerilimi, akıma göre 90 derece geridedir.Burada da
önceki devrede olduğu gibi aynı yöntemle

Cos j =  R / Z                 ve

          _____________

Z = V R² + XC²       bulunur.         

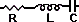
Direnç üzerinde gerilim akıma göre değişmez demiştik.

Bobinin gerilimi 90 derecede ileride, Kondansatörün gerilimi 

ise 90 derece geridedir. Bu devrenin diyagramı şu şekilde gösterilir.

Bobin ve kondansatörün Reaktansları görüldüğü gibi birbirlerinezıt yöndedir,
bu nedenle bu iki reaktansın farkı ile rezistansın vektörel toplamları bize
devrenin empedansını verir.

Burada 

XL > XC den büyük ise devre indüktif tir.

XC > XL den büyük ise devre kapasitiftir.

Eğer  XL = XC ise rezonans durumu söz konusudur. Yani devre alternatif akımın
salınımına en az direnci gösterir.Burada empedans yanlızca rezistansa eşit olur.

Cos j = R / Z            dir.

İndüktans ile Kapasitans arasındaki fark  D X ise Empedans:

         ________________

Z= V R²  +  D X²          olur.

Bobin ve Kondansatörün paralel olduğu devrelerde, referans gerilimdir; çünkü
gerilim paralel devre elemanlarının uçlarında aynıdır, değişmez. Bu devrelere
gerilim devreleri denir.

 

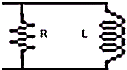Direnç Bobin Paralel devresi

 

 Bir direnç ve bir bobin paralel bağlı ise, direnç üzerinde akım ve gerilim
arasında faz farkı yoktur.Bobin üzerinde ise akım gerilimegöre 90 derece
geridedir.

Devrenin toplam akımı akımların vektörel toplamlarına eşittir.

Bir direnç ile bir kondansatör paralel bağlı olduğunda kondansatörde akım 90
derece ileridedir ve 8 nolu formülde XL yerine XC konur.

Direnç Bobin ve kondansatör birlikte ise Empedans

 

Seri devrelerde rezonans halinde X_L =  X_C olduğu için
bu devrelerde empedans  minimumdur,empedans minimum olduğunda akım maksimum olur

Paralel rezonans devrelerinde ise  rezonans halinde durum tam tersidir ve
akım minimum, empedans maximumdur.

Rezonans halinde, maksimum akımın 0.7'si kadar akım değerlerine denk gelen
D f aralığına da 'Bant genişliği' adı verilir.

Bant genişliğinin az olması devrenin 'Q' kalite faktörünün yüksekliği
anlamına gelir.

Q = XL / R